Definition
The theory of AC (Alternative Current) rotating machines considers sinusoidal supply currents, but in reality it is usually composed of an addition of multiple harmonics. For a given phase, the current waveform can be written as:

With:
-
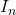 the amplitude of the harmonic
the amplitude of the harmonic -
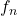 the frequency of the harmonic (
the frequency of the harmonic ( is the fundamental electrical frequency )
is the fundamental electrical frequency )  the phase of the harmonic
the phase of the harmonic


Figure 1: Waveform and spectrum of a sinusoidal current


Figure 2: Waveform and spectrum of a non sinusoidal current
Different physical phenomena lead to the creation of these harmonics:
- Supply voltage harmonics due to Pulse Width Modulation (PWM) or six-step operation
- Control harmonics induced on purpose to reduce magnetic noise (Harmonic Current Injection) or to increase average torque or efficiency
- Voltage harmonics induced by magnetic flux harmonics (e.g. back emf in PMSM, Rotor Slot Harmonic in IM) due to strong electrical to magnetic coupling
- Voltage harmonics introduced by non-linearities of the inverter or power converter
- DC voltage ripple
- Current ripple introduced by resolver inaccuracy in synchronous machines
These sources of harmonics may be found when measuring the current / voltage waveforms of an electric drive.
Application to e-NVH
Additional current harmonics create additional flux harmonics, which in turn create additional force harmonics. Current harmonics mainly induce additional magnetic forces of wavenumber 0 and 2p (number of poles). This additional forces can result in additional magnetic noise and vibration, especially when they resonate with a structural mode of the electric drive.
Application to Manatee
In Manatee e-NVH software, current harmonics can be defined as an input of a current-driven simulation. Sensitivity study and multi-objective optimization can be run on 6fe, 12fe and 18fe current harmonics as well. Finally, a specific Harmonic Current Injection environment dedicated to noise reduction is provided. In Manatee the current harmonics are defined by an amplitude and a phase relative to the fundamental. The current is computed with the following equation:

With :
-
 the amplitude of the fundamental computed via Id and Iq
the amplitude of the fundamental computed via Id and Iq -
 the frequency of the fundamental (stator current electrical frequency)
the frequency of the fundamental (stator current electrical frequency) -
 the phase of the fundamental
the phase of the fundamental -
 the rank of the harmonic
the rank of the harmonic -
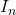 the amplitude of the harmonic with the rank n
the amplitude of the harmonic with the rank n -
 the relative phase of the harmonic with the rank n
the relative phase of the harmonic with the rank n -
 the number of harmonics defined by the user
the number of harmonics defined by the user